 Anyone interested in the GMO debate has probably heard about the Seralini paper that I criticized a while back. That paper was eventually retracted by the original journal, and it has now been re-published in a different journal. There are quite a few articles describing the background, so I won’t get into those details. I suggest reading recent pieces at Retraction Watch or Grist if you want to get the background information.
Anyone interested in the GMO debate has probably heard about the Seralini paper that I criticized a while back. That paper was eventually retracted by the original journal, and it has now been re-published in a different journal. There are quite a few articles describing the background, so I won’t get into those details. I suggest reading recent pieces at Retraction Watch or Grist if you want to get the background information.
The Seralini press release for the re-published article states “The raw data underlying the study’s findings are also published” and this claim has been reprinted by many sources without much scrutiny. For example, the Nature News coverage states that “The authors also published their raw data; Séralini says that he wanted to be a paragon of transparency, and hopes that companies making and selling genetically modified (GM) food will follow his example.”
After a very brief examination of the data files supplied by Seralini’s team, it is clear that they didn’t actually provide all of their raw data. Nathanael Johnson, who has become one of my most trusted journalists on the topic of GMOs also initially praised Seralini’s team for releasing their raw data. To Johnson’s credit, he updated his post when it was pointed out that the data Seralini’s team released was not really the “raw data.”
A line in this piece originally read, “In republishing the paper, Séralini and his team released their raw data, for which they deserve tremendous credit.” That’s not quite right. It turns out that the Séralini group did not release all the raw data from the study. For instance, his team took blood samples at 1, 2, 3, 6, 9, 12, 15, 18, 21, and 24 months but only released the data for month 15. They released the tumor and mortality data for each group of rats, but not for the individual rats — which makes it impossible to test for in-group variation (e.g. are we talking about one rat with seven tumors, or seven rats with one tumor each?). -Nathanael Johnson at Grist
Johnson, in his Grist piece, suggests that even though the statistics in the paper have been criticized heavily, the Seralini study “deserves to be taken seriously, and considered along with all the other other good, independently funded science on GM safety.” I resisted writing a post on this for a while, since I didn’t really think it would be worth the time. In all honesty, it probably wasn’t worth the time. But because there has now been some data released, well, FREE DATA! Curiosity got the better of me. As Johnson notes, the tumor data Seralini’s team released is pretty worthless in terms of being able to draw any conclusions. Without data on each rat, a simple count of the number of tumors on a group of 10 rats isn’t very informative, so I didn’t bother with that data. In his piece, Johnson suggests:
“But what if we ignore the tumors and focus on organ damage and mortality?”
This seems to me like a reasonable place to start. There are no data provided that support any of the statements or conclusions in the section titled “Anatomopathological observations and liver parameters” so nothing we can evaluate there. But we can look through the mortality and biochemistry data.
[NOTE: to keep this post readable, I’ve edited and highlighted the code/results to only include the necessary information. If you want all the gory details, the entire analysis can be viewed here.]
Mortality Data
As a disclaimer, I am not an expert in survival analysis, so I would welcome criticism or comments from those more familiar with this type of analysis. Based on what I could gather, the mortality data released by Seralini was in somewhat of a non-standard format for time to mortality data. I reformatted the data into something I could work with, and have posted the reformatted data in case anyone wants to double check my work.
## Group Sex Treatment Rat time mortality
## 1 All Male Control A 493 1
## 2 All Male Control B 574 1
## 3 All Male Control C 588 1
## 4 All Male Control D 604 1
## 5 All Male Control E 610 1
## 6 All Male Control F 632 1I’ve reformatted the data to include the Sex, Treatment, Rat (experimental unit, 10 per treatment), time, and mortality. The mortality column indicates 1 for death, and 0 for still alive. Each rat that died during the experiment has a value of 1 for mortality that corresponds to the time that it died (in days). For the first few control rats in the data set, they died on day 493, 574, 588, etc. If the rat lived for the duration of the study, then it has a 0 in the mortality column that corresponds to day 720, or the end of the experiment.
I then used this file to run a survival analysis on the data. Honestly, I’m not sure which is most appropriate model for such small sample sizes, but a very quick search found that the Cox proportional hazards model has been used to look at the effect of diet on rats. Any readers with experience with survival analysis are welcome to suggest a better method.
## Male survival analysis:
summary(coxph(Surv(time,mortality)~Treatment, data=morts.m))## n= 100, number of events= 74
## coef exp(coef) se(coef) z Pr(>|z|)
## TreatmentGMO.11 -0.197 0.821 0.507 -0.39 0.697
## TreatmentGMO.11.R -0.356 0.700 0.506 -0.70 0.481
## TreatmentGMO.22 -0.615 0.541 0.506 -1.22 0.224
## TreatmentGMO.22.R -0.317 0.728 0.507 -0.63 0.531
## TreatmentGMO.33 -0.898 0.407 0.530 -1.70 0.090 .
## TreatmentGMO.33.R 0.152 1.164 0.460 0.33 0.742
## TreatmentRa -0.287 0.750 0.487 -0.59 0.555
## TreatmentRb -0.521 0.594 0.506 -1.03 0.304
## TreatmentRc -0.916 0.400 0.530 -1.73 0.084 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Likelihood ratio test= 8.17 on 9 df, p=0.517
## Wald test = 8 on 9 df, p=0.535
## Score (logrank) test = 8.36 on 9 df, p=0.498For the male rats, there appears to be no strong evidence that their diet influenced mortality. The last 3 lines of the output show p-values ranging from 0.498 to 0.535; results that appear to be consistent with chance. We get similar results looking at the Female rats:
## Female survival analysis:
summary(coxph(Surv(time,mortality)~Treatment, data=morts.f))## n= 100, number of events= 49
## coef exp(coef) se(coef) z Pr(>|z|)
## TreatmentGMO.11 0.698 2.010 0.866 0.81 0.420
## TreatmentGMO.11.R 1.053 2.867 0.837 1.26 0.208
## TreatmentGMO.22 1.586 4.883 0.817 1.94 0.052 .
## TreatmentGMO.22.R 1.630 5.102 0.804 2.03 0.043 *
## TreatmentGMO.33 1.399 4.050 0.817 1.71 0.087 .
## TreatmentGMO.33.R 0.850 2.340 0.866 0.98 0.327
## TreatmentRa 1.308 3.700 0.817 1.60 0.109
## TreatmentRb 0.875 2.398 0.866 1.01 0.313
## TreatmentRc 1.150 3.158 0.837 1.37 0.169
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Likelihood ratio test= 8.43 on 9 df, p=0.491
## Wald test = 7.36 on 9 df, p=0.599
## Score (logrank) test = 8.06 on 9 df, p=0.528For the females, P-values range from 0.491 to 0.528 depending on the test. Again, very little evidence here that the diets had much impact on mortality. Now if we ignore the overall P-value and focus only on individual treatments (generally a bad idea, but humor me), there are some P-values that indicate there were some treatments that may be different from the control. For female rats, the 22% GMO diet + Roundup has a P-value of 0.043, indicating the proportional hazard is “significantly” different from the control. Interpretation of the coeficients from survival analysis is not exactly straightforward, but because the exp(coef) column is greater than 1, then we would interpret that to mean the rats on that diet are more likely to die compared to control rats. If we ignore the P-values altogether, we can see that all of the exp(coef) are greater than 1. So if we ignore the variability in the data, we could interpret this to mean that the female rats are more likely to die from all the treatments, compared to the control. And this is basically what Seralini has done in the article, by stating in the abstract: “In females, all treatment groups showed a two- to threefold increase in mortality, and deaths were earlier.”
But if we’re willing to ignore the statistics to draw this conclusion for females, then it seems only fair that we should do the same for the males. And if we look at the exp(coef) for the male rats, all but one treatment is less than 1. This would indicate that all except 1 treatment reduced the hazard to male rats. I didn’t see this as a headline in any of the press releases. Again, I’m not a rat expert, but I can’t really think of any mechanism by which both GMO feed and Roundup in drinking water would have a negative effect on females but a positive effect on males.
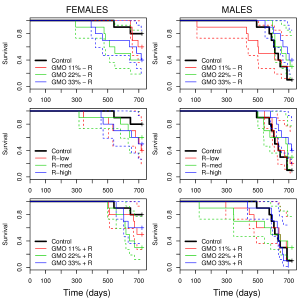
I’ve re-created Seralini’s Figure 6 from the article (click figure to embiggen), but I’ve used color and added the 95% confidence intervals for each treatment. The solid lines are the same as those included by Seralini (except decreasing survival instead of increasing mortality), and the dotted lines indicate the 95% confidence intervals for each treatment. The thing to notice is that the confidence intervals for all treatments (dotted colored lines) surround the control group (thick black line). The data Seralini provided simply doesn’t support a link between GMOs or Roundup laced diet and premature death. This doesn’t mean that the diets had no effect; it is certainly possible that the GMO or Roundup diets caused Females to die earlier (or even that the GMO diets caused males to live longer). What this means is that the mortality data provided by Seralini are simply not powerful enough to draw any conclusions one way or the other. Which is basically the same problem many folks identified with this study early on, even without the data in hand.
Body Weight
Interestingly, there is a column in the biochemistry data named “BW.15” which does not show up in any of the description files, and is also never referenced in the published article. I’m guessing here, but it seems like BW is a logical abbreviation for body weight. I’ve sent an email to Dr. Seralini to confirm that BW is an abbreviation for body weight, and will update the post if I hear back from him (I’m not holding my breath). Update: I have received confirmation from someone at King’s College London School of Medicine that the “BW.15” column is indeed body weight at 15 months. The only reference to body weight in the republished article is near the beginning of the results section:
There was no rejection by the animals of the diet with or without GM maize, nor any major difference in body weight (data not shown).
If the BW variable in the provided data is body weight, I question the interpretation of no “major difference in body weight.”
Female:
## Df Sum Sq Mean Sq F value Pr(>F)
## TRT 9 53684 5965 2.07 0.041 *
## Residuals 84 241850 2879
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## TRT mean(BW.15)
## 1 Control_F 405.6
## 2 C-RupA_F 414.0
## 3 C-RupB_F 390.4
## 4 C-RupC_F 327.1
## 5 GMO11_F 397.1
## 6 GMO11+R_F 397.2
## 7 GMO22_F 383.4
## 8 GMO22+R_F 413.8
## 9 GMO33_F 393.2
## 10 GMO33+R_F 411.8Tukey's HSD comparisons with P<0.10
## diff lwr upr p adj
## C-RupC_F-Control_F -78.52 -158.657 1.608 0.05961
## C-RupC_F-C-RupA_F -86.93 -169.147 -4.719 0.02956
## GMO22+R_F-C-RupC_F 86.72 6.592 166.857 0.02331
## GMO33+R_F-C-RupC_F 84.72 4.592 164.857 0.02959For the female rats, there was a significant difference between treatments with respect to the BW variable. The highest dose of Roundup in drinking water (coded in the csv file by me as C-RupC) reduced BW by 19% compared to the control group. This difference was right on the border of what would generally be considered “significant” (P=0.059), but the difference was significant for several other comparisons with the high Roundup dose. For the males, there was a very similar pattern:
Male:
## Df Sum Sq Mean Sq F value Pr(>F)
## TRT 9 163282 18142 4.2 0.00018 ***
## Residuals 81 349928 4320
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## TRT mean(BW.15)
## 1 Control_M 673.5
## 2 C-RupA_M 621.3
## 3 C-RupB_M 623.6
## 4 C-RupC_M 518.6
## 5 GMO11_M 658.2
## 6 GMO11+R_M 639.0
## 7 GMO22_M 648.0
## 8 GMO22+R_M 618.2
## 9 GMO33_M 659.7
## 10 GMO33+R_M 623.6Tukey's HSD comparisons with P-value<0.10
## diff lwr upr p adj
## C-RupC_M-Control_M -154.92 -250.554 -59.286 4.688e-05
## C-RupC_M-C-RupA_M -102.70 -198.334 -7.066 2.532e-02
## C-RupC_M-C-RupB_M -104.98 -200.614 -9.346 2.010e-02
## GMO11_M-C-RupC_M 139.61 34.226 244.994 1.776e-03
## GMO11+R_M-C-RupC_M 120.43 19.000 221.870 8.089e-03
## GMO22_M-C-RupC_M 129.41 33.776 225.044 1.278e-03
## GMO22+R_M-C-RupC_M 99.65 -5.731 205.037 7.962e-02
## GMO33_M-C-RupC_M 141.10 45.466 236.734 2.937e-04
## GMO33+R_M-C-RupC_M 105.04 6.789 203.298 2.650e-02The high dose of Roundup in the drinking water reduced male BW by 23%. The high-dose Roundup treatment was significantly different from nearly all of the other treatments, including the control. So my conclusion here would be that drinking a 0.5% Roundup solution every day for 15 months will reduce body weight. I can’t quite figure out why the Seralini article didn’t report this very obvious difference (in fact, they made the opposite claim, that there were no differences).
There are twois really only one possible explanation for this discrepancy: If the BW variable actually is rat body weight, then Seralini et al. mischaracterize their data when they state there were no “major differences in body weight (data not shown).” I would argue a 20% reduction in body weight by a treatment is a major difference. The other explanation is that the BW variable in the data file they’ve provided isn’t actually body weight. But I can find no reference to what BW might otherwise be in the article itself or any of the supplemental information. Now, I’m not going to speculate why Seralini would state there were no differences in body weight when the differences were this dramatic, but it does seem very odd.
Biochemistry Data
Although the methods section in the paper states that blood samples were taken 10 different times over the course of the study, the paper only presents data from one time point (15 months). The 15 month data is also the only time point provided in the supplemental materials. In the paper, Seralini et al. justify presenting only a single time point by saying:
“Due to the large quantity of data collected, it cannot all be shown in one report, but we present here the most important findings.”
Even if true for the actual article, I really don’t see how this restriction would apply to the raw data. It seems like they could have easily added data from the other 9 time points into the same Excel file and provided all the raw data quite easily. But they have not, so it is impossible to tell whether the 15 month data are representative, or if this time point was simply the ‘best’ time point for some purpose. The easiest way to counter the early accusations of “cherry picking” data would be to release the rest of the data. But I doubt that a request from a small Wyoming weed blog will prompt additional data release.
As I read through the statistical methods section of the article for the biochemistry data analysis, I was reminded how complex the analysis of the biochemistry data was. I have to agree with Marion Nestle’s assessment that it was “weirdly complicated.” I have dabbled in multivariate analyses before, and understand the basics of principal component and discriminant analysis (which they reference), but I really have no idea how to implement an OLPS-DA analysis. So I’m not going to even attempt to recreate their multivariate analysis. If anyone has experience with this analysis, I’d be interested to see them re-create and interpret the newly released data.
But we can at least run some more standard statistical tests for some of the variables. In particular, I was interested in some of the variables that Seralini’s multivariate analysis suggested were important. I’ll admit, the top half of Seralini’s Figure 3 confused me almost as much as the description of the multivariate methods. (For example, I still don’t understand why on earth they decided to present “On X axis, animals;” I guess this means each animal is represented by one point on the line.  But what an odd way to present the data. Line charts are typically reserved for data where there is a continuous variable on the x-axis, but I don’t think there’s any reason to think there is an increasing or decreasing order to the rats within a treatment. I mean, placing individuals on the x-axis doesn’t really make any sense. Also, I’m pretty sure this is the first time I’ve included a figure in a parenthetical thought. But I digress. A lot.)
But what an odd way to present the data. Line charts are typically reserved for data where there is a continuous variable on the x-axis, but I don’t think there’s any reason to think there is an increasing or decreasing order to the rats within a treatment. I mean, placing individuals on the x-axis doesn’t really make any sense. Also, I’m pretty sure this is the first time I’ve included a figure in a parenthetical thought. But I digress. A lot.)
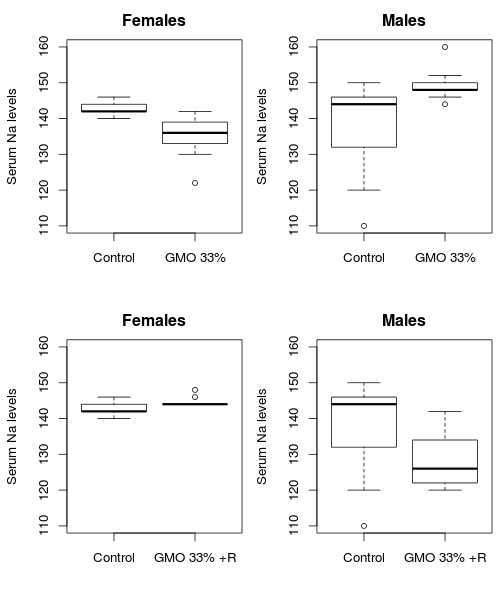
From what I can understand from Seralini’s Figure 3 caption, they only compared the control group with the 33% GMO group, and only for females. I can’t find an explanation for why they chose only one of the treatments and one sex for this analysis; perhaps it was again due to space constraints. Seralini uses Figure 3 to conclude “Profiles evidence kidney ion leakages and sex hormonal imbalance versus controls.” Again, I don’t know much about mammalian physiology, so I did a quick google scholar search for “kidney ion leakage.” That returned no results, so I repeated the search without quotation marks. The ions referenced in recent papers are all over the board, Na+, K+, Cl-, H+, and even many metal ions. Seralini shows both blood serum and urine excreted Na and Cl ions in the figure, and if I’m interpreting the bottom half of figure 3 correctly, those ions had the most predictive effect in the analysis. So it certainly seems worth looking at those ions using a more standard test. Starting with Na, I ran a t-test to compare the same two groups as Seralini, the GMO 33% diet with the control.
## Welch Two Sample t-test
##
## "Control_F" vs. "GMO33_F"
## t = 3.019, df = 6.517, p-value = 0.02118
## Control GMO 33%
## 142.8 134.9The GMO 33% treatment had a serum sodium level about 5.5% lower than the control group (P=0.02). This does seem consistent with Seralini’s results. But what about male rats, which Seralini didn’t present?
## Welch Two Sample t-test
##
## "Control_M"] vs. "GMO33_M"
## t = -2.661, df = 10.89, p-value = 0.02233
## Control GMO 33%
## 137.4 149.2There also appears to be a significant difference between the control group and the GMO 33% diet for males (P=0.02). But, the difference is in the opposite direction! The 33% GMO diet that reduced blood sodium levels in females, apparently increased the blood serum sodium levels in males by 8.6%. I’m not sure which of these relates to kidney ion leakage, but it seems that both an increase and a decrease in the same ion can’t be indicative of the same problem.
Because of the structure of the experiment, we should be able to confirm these results by looking at two other treatments; both sexes were also fed the 33% GMO diet that had been treated in the field with Roundup. I would expect that any effect of the GMO that hadn’t been treated with Roundup should still exist if the corn had been sprayed with Roundup. So I compared these treatments with the controls to confirm the results were due to treatment and not random variability.
## Welch Two Sample t-test
##
## "Control_F" vs. "GMO33+R_F"
## t = -2.635, df = 17.18, p-value = 0.01727
## Control GMO33%+R
## 142.8 144.6## Welch Two Sample t-test
##
## "Control_M" vs. "GMO33+R_M"
## t = 1.825, df = 14.47, p-value = 0.08878
## Control GMO 33%+R
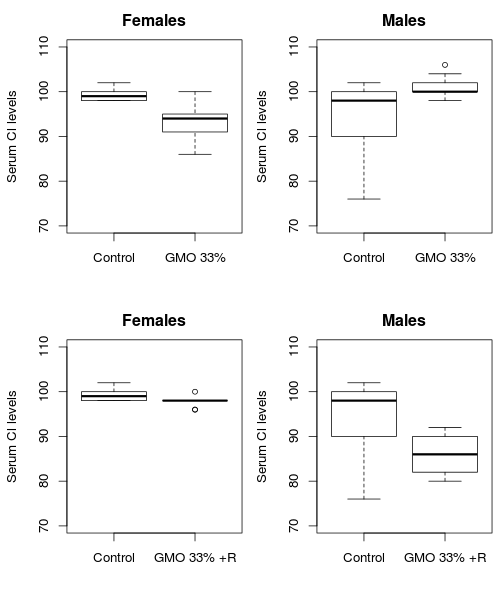
## 137.4 128.4Somehow, spraying Roundup on the GMO corn in the field reversed the blood serum sodium level results. In both sexes. I can think of absolutely no reasonable explanation for this result other than random chance. And analysis of the blood serum chloride shows similarly random results:
Based on the released data I’ve looked through, I can see no reasonable, consistent relationship between the experimental treatments and the response variables in the newly released data. Granted, I’ve not taken the time to look at every response presented in the released data. And I’ve also not tried to run any multivariate analyses yet. But the variables Seralini et al. found to be most important in their multivariate analysis seem to be mostly meaningless if you look at more than the two groups they present. I think it is also important to note that Seralini et al. state that the data presented in their article (and therefore the data they released) represents “the most important findings.” So if we can’t make any sense of the most important findings using a reasonable statistical analysis, I really don’t see how there is any real reason why this study, as presented, “deserves to be taken seriously.”
UPDATE (July 9, 2014): the attached analysis now includes all possible pairwise comparisons (4,320 total) with the released biochemistry data. Analyzing the data this way is the very definition of a “fishing expedition,” and this method is almost certain to lead to finding “statistical” differences that are meaningless. But I wanted to really look at the data to see if any obvious patterns emerged. To summarize those results, only 7% of the possible comparisons were “significant” if we use the standard cutoff value of P=0.05. Most statisticians agree that 0.05 is a pretty arbitrary cutoff, but it is probably the most standard value for “significance.” When we use P=0.05 as our cutoff value for “significant” differences, we can expect that about 5% of the observed “significant” differences to have occured by chance. So these results are very much consistent with what we’d expect purely by chance.
Also of note: 119 of the “significant” differences involved the high-dose Roundup in the drinking water treatment. This treatment is really not very interesting because we already know that if a rat is given nothing to drink but a commercially formulated pesticide, it is probably not going to fare well. So 39% of the “significant” differences are due to a treatment that isn’t even remotely relevant to real world use of GMOs or pesticides. Unless you plan to drink formulated Roundup at commercial application rates every day for the rest of your life. If you exclude this treatment, my guess is many of the “significant” differences would go away.
And finally, only 47 of the “significant” comparisons were between a treatment and the control group (or about 1.1% of the possible comparisons). The whole reason for using a control group is to compare the treatments against. And these differences were scattered throughout the data set, with no obvious patterns that I could find (except perhaps differences with the above-referenced high dose Roundup treatment).


Comments are closed.